На плоскости заданы n прямых,
никакие две из которых не лежат на
одной прямой и никакие три — на
одной окружности.
страшный сон
Именно столько баллов надо было набрать победителю краевого этапа российской олимпиады по математике, чтобы получить право выступать на всероссийском этапе.
Эта самая олимпиада — дело традиционное. Всё началось в далёком 1935 году, когда в Ленинграде по инициативе и под руководством члена-корреспондента АН СССР Льва Генриховича Шнирельмана была организована самая первая в СССР олимпиада для школьников по математике. И вот вся эта история тянется до сих пор; вообще, разных олимпиад расплодилось какое-то безумное множество и значительная их часть есть просто один из честных способов отъёма денег у населения, но та олимпиада, которую организует и проводит Министерство образования и науки РФ, всё же держит марку. По крайней мере, в области математики.
Министерская олимпиада устроена по пирамидальному принципу: сперва в школах — но это сильно опционально. Некоторые школы проводят, некоторые нет. Потом районный этап. Потом (в некоторых крупных городах) городской. Потом региональный; в нашем случае — краевой. И потом уже всероссийский. А на закуску — участие в международной олимпиаде.
Так вот, в прошедшие выходные был краевой этап олимпиады по математике. Среди 9-х, 10-х и 11-х классов. Ну, одиннадцатые классы меня совершенно не интересовали (точнее, постольку-поскольку), и в результате стал я членом жюри в девятых классах. В смысле — членом-то я был «всеобщего» жюри, а вот проверял решения задач в девятом классе.
Итак, сорок два. Именно столько, повторюсь, надо набрать участнику олимпиады за два тура (при возможном максимуме в 56 баллов), чтобы получить право поехать на всероссийский этап. Увы. Ни в одном классе (с 9-го по 11-ый) никто столько заветных баллов не набрал. Малоприятная ситуация: в былые годы набирали и представляли наш край на всероссийском этапе. А нынче нет, не получилось.
Причины этого разные. Начнём с банальных; как мне кажется, задачи были сложноваты. Это само по себе и не грех, но не очень эффективно. Если вы хотите «измерить» уровень математических способностей 50 человек и для этого предлагаете им решить пять задач, а результаты таковы, что лишь пятеро решило три задачи, а остальные — одну и меньше, то, согласитесь, ваш инструмент весьма беден: он «отмеряет» лишь самых-самых сильных. Примерно это и случилось в нынешнем году — смотри для примера обе задачи. По моему глубокому убеждению, головной московский штаб достаточно расслабленно подошёл к написанию собственно формулировок. Они не то чтобы сложны, но ужасно непрозрачны. Так, например, жюри (ну, четверо человек, если быть точным) пришло к правильному пониманию условия лишь за двадцать минут бурных дебатов. Согласитесь, бурно дебатировать всегда более продуктивно, чем в одиночку пробиваться через формулировки. Соответственно, по моему личному мнению, составители задач этого года украли у участников примерно по пятнадцать — двадцать минут на том, что дали мудрёные формулировки. Ну, да бог с ним! Имеют право, в конце концов. К тому же, эти формулировки были совершенно теми же по всей стране и ситуация в этой части была совершенно справедливой.
Но есть и более печальные причины. Системные. Я отчётливо помню времена, когда местные теоретики образования (имевшие немалый вес среди управленцев) на полном серьёзе объясняли нам, обычным учителям, что предметные олимпиады — это такое зло, которое надо всеми силами обегать. А зло оно у них потому что, по их словам, олимпиады подавляют фантазию и способность детей к творчеству. Я, грешным делом, и тогда, и сейчас убеждён, что главной причиной такого их отрицательного отношения к олимпиадам является их полная и катастрофическая неспособность решить хотя бы простую олимпиадную задачу хотя бы для 5-го класса. Но по факту мы имеем в крае скорее печальную ситуацию.
Дело в том, что школьные предметные олимпиады сродни спорту так называемых высоких достижений. Очевидно, что чемпионом мира или (спортивных) Олимпийских Игр станет очень и очень не каждый перворазрядник. И уж тем более, не третьеразрядник. Очевидно, что кроме того, что лишь немногие доберутся до высоких достижений, а большинство по пути отсеется и никогда не проявит себя как сколько-нибудь значимый спортсмен, есть ещё масса всяких ухищрений, в основном медико-биологического характера. Но не об этом речь. А о том, что если вы хотите, чтобы в вашей стране были победители Олимпийских Игр, вы вынуждены всё начинать с самого низа: с массового «дворового» спорта. Другого способа нет. Увы. И ровно та же ситуация с олимпиадами по школьным предметам.
Наш край уже который год благополучно переживает острейший кризис в этой области. Кризис усугублен ещё и тем, что нынче огромное количество самых разных соревнований и утех, именуемых гордым словом «олимпиада», и простому школьнику крайне сложно понять, что там стоящее, а что — на лужайке детский лепет. Если руководство края хочет, чтобы наш край был устойчиво и достойно представлен на всероссийском этапе предметных олимпиад, то оно должно принять ряд простых и действенных мер. Например, повелеть проводить массовые школьные олимпиады начиная с пятого класса. Чтобы можно было найти наиболее перспективных школьников. А, кроме того, как и в спорте высших достижений, потом с отобранными специально работать: сборы, тренировки, ещё сборы и прочие разминки с упражнениями.
Ну, а пока наш край озабочен лишь спортом: на носу — хорошо, не на самом носу, но всё равно не так и далеко Универсиада... Увы, насколько я понимаю, никакого сколько-нибудь интеллектуального (в смысле, не связанного напрямую со спортом) вида соревнований там не планируется.
Сегодня только две задачи. Поскольку сложные. В точности, ровно те, что были на краевой олимпиаде по математике во втором туре (он традиционно считается попроще; хотя в наше время было наоборот).
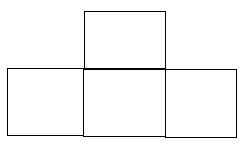
- В клетках доски 8 и 8 расставлены числа 1 и —1 (в каждой клетке — по одному числу). Рассмотрим всевозможные расположения фигурки (см. рисунок ниже) на доске (фигурку можно поворачивать, но её клетки не должны выходить за пределы доски). Назовём такое расположение неудачным, если сумма чисел, стоящих в четырёх клетках фигурки, не равна 0. Найдите наименьшее возможное число неудачных расположений.
- Тридцать девочек — 13 в красных платьях и 17 в синих платьях — водили хоровод вокруг новогодней ёлки. Впоследствии каждую из них спросили, была ли её соседка справа в синем платье. Оказалось, что правильно ответили те и только те девочки, которые стояли между девочками в платьях одного цвета. Сколько девочек могли ответить утвердительно?
Михаил Садовский